kvant_on_maplenet

1 1970

Ежемесячный
научно-популярный
физико-математический
журнал

II ЦЕПНЫЕ ДРОБИ

3. Понятие о цепной дроби

Забудем о десятичной системе счисления. Как говорил выдающийся русский математик Николай Николаевич Лузин (1883-1950), "преимущества десятичной системы не математические, а зоологические. Если бы, у нас на руках было не десять пальцев, а восемь, то человечество пользовалось бы восьмеричной системой". Десятичная система практически очень удобна, но при исследовании теоретических вопросов арифметики она только мешает.

Итак, откажемся от специальных систем счисления, и задумаемся над вопросом: какой самый естественный способ приближенного представления положительных чисел дробями.
В ответе на этот вопрос не может быть никаких колебаний: надо прежде всего указать, между какими целыми числами оно заключено. Например,

Разумеется, достаточно указывать только меньшее из этих чисел:

Заметим, что такая оценка не связана со способом обозначения целых чисел, т. е. с какой-нибудь конкретной системой счисления.
Займемся числом . Наша оценка "два с лишним" слишком грубая и годится лишь как первое приближение. Если мы хотим сделать второй шаг, то мы должны оценить добавку х . Поскольку она меньше единицы, естественно представить ее как дробь с числителем 1 (мы опять апеллируем к "естественности", но это - в последний раз)

Теперь x₁ больше единицы, и мы опять повторяем те же шаги: выделяем целую часть и т. д. и т. д. Приглашаем читателя внимательно проследить за чередованием этих двух шагов:

Выражение

где a₁ , a₂ , ... , a_s - натуральные числа , а a₀ - натуральное число или нуль, называется цепной дробью .
Числа a₀ , a₁ , a₂ ,..., a_s называются элементами * цепной дроби.

Иногда их называют неполными частными.

Не слишком ли громоздко обозначение цепной дроби? В нашем примере получилась трехэтажная дробь, а если получится двадцатиэтажная, то ее нельзя уместить на листе бумаги.
Это верно, и поэтому для цепных дробей употребляются различные условные обозначения. Мы будем пользоваться таким:

(*)

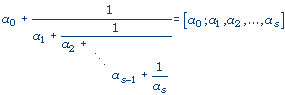
Обратите внимание на точку с запятой. Она подчеркивает, что роль целой части a₀ особая, не такая, как других чисел (особая - не значит более важная, в данном случае скорее наоборот).

Можно ли утверждать, что всякое действительное *) число может быть изображено цепной дробью и притом единственным образом?

* ) Пока речь идет о положительных рациональных числах. Введение отрицательных чисел ничего не меняет в существе вопроса, а введение иррациональных чисел многое меняет. Об этом будет сказано ниже.

Прежде всего задумаемся над таким примером:

или, в сокращенных обозначениях,

[0;6,4] = [0;6,3,1],

Такое преобразование (отделение единицы от последнего элемента) можно произвести с любой цепной дробью, у которой последний элемент отличен от единицы. Если же последний элемент равен единице, то его можно прибавить к предпоследнему. Например,

[1;10,3,7,1] = [1;10,3,8].

Легко, однако, доказать, что это - единственная причина неоднозначности представления рационального числа цепной дробью.

Можно доказать, что:

1) Процесс превращения рационального числа p/q (р и q взаимно простые натуральные числа) в цепную дробь на некотором шаге заканчивается. Иначе говоря, любое положительное рациональное число представимо в виде (*). В силу только что сказанного такое представление всегда возможно и с соблюдением ограничения a_s>1 .

2) Две цепные дроби [a₀;a₁,...,a_s] и [b₀;b₁,...,b_t] , у которых a_s>1 и b_t >1 , равны друг другу в том и только в том случае, если у них одинаковое число элементов, т. е. s = t и a _i= b_i при i = 1, 2, . . ., s .

Мы этого доказывать не будем. Цель нашей статьи в том, чтобы рассказать основные идеи и побудить читателя к более основательному изучению вопроса по книгам *).

Все пропущенные здесь доказательства можно найти, например, в книжке А. Я. X и н ч и н а "Цепные дроби", изд. 3, 1961.

4. Бесконечные цепные дроби

А как быть с иррациональными числами? Попробуем разлагать в цепную дробь

Получим

, ,

Ясно, что

где .

Хочется сразу написать

т. е. представить в виде бесконечной цепной дроби . Но здесь нужна крайняя осторожность: мы встретились с новым понятием "бесконечная десятичная дробь", но не знаем, что это такое. Легко понять только, что каждому положительному иррациональному числу с о о т в е т с т в у е т вполне определенная бесконечная последовательность

где a ₀ - целое не отрицательное, а все a _i с номером - натуральные числа. Во всем относящемся сюда мы разберемся только позже *), а пока удовлетворимся тем, что нам понятно: как по положительному числу построить его формальное разложение

в конечную или бесконечную цепную дробь **).

Этот вопрос будет полностью рассмотрен в одном из следующих номеров журнала.

"~"-знак соответствия. Мы боимся поставить знак равенства, пока не установлен смысл символа, стоящего в правой части.

5. Подходящие дроби

Цепную дробь можно оборвать, удержав элементы a ₀ , a ₁ , ... , a _n и отбросив a _n+1 ,... Полученное таким образом число называется n -й подходящей дробью и обозначается .

В частности, при n = 0 имеем нулевую подходящую дробь

Мы увидим, что, чем меньше n , тем подходящая дробь проще (т. е. имеет меньший знаменатель). В то же время она может использоваться как приближенное значение цепной дроби.

Пример

Возьмем опять разложение числа в цепную дробь и образуем подходящие дроби

Разумеется, последняя подходящая дробь рационального числа a равна a .

Мы получили несколько постепенно усложняющихся приближений для числа

Для оценки их заметим, что

*).

- погрешность (см. стр. 17).

Мы замечаем, что погрешность убывает (по абсолютной величине) и имеет чередующиеся знаки. Это - общее правило.
В случае разложения в цепную дробь числа получим

Мы наблюдаем и здесь ту же самую картину.

6. Основное свойство подходящих дробей

Сформулируем теперь без доказательства то основное свойство подходящих дробей, которое и приведет к разгадкам наших загадок.

Если

- подходящая дробь для числа , то абсолютная погрешность

меньше, чем при аппроксимации числа любой другой дробью с меньшим знаменателем *).

Подходящие дроби во многих отношениях дают чрезвычайно выгодные приближения. Приведенное здесь свойство - не единственное и не самое главное. Другие свойства будут рассмотрены в одном из следующих номеров журнала.

Например, получив для подходящую дробь , мы можем быть уверены, что приближение к любой дроби со знаменателем, меньшим 12, будет хуже.

Глава I

Глава II

Глава III

Задачи

maplenet 2226

valery